Algorithm Note - Binary Search Tree (BST)
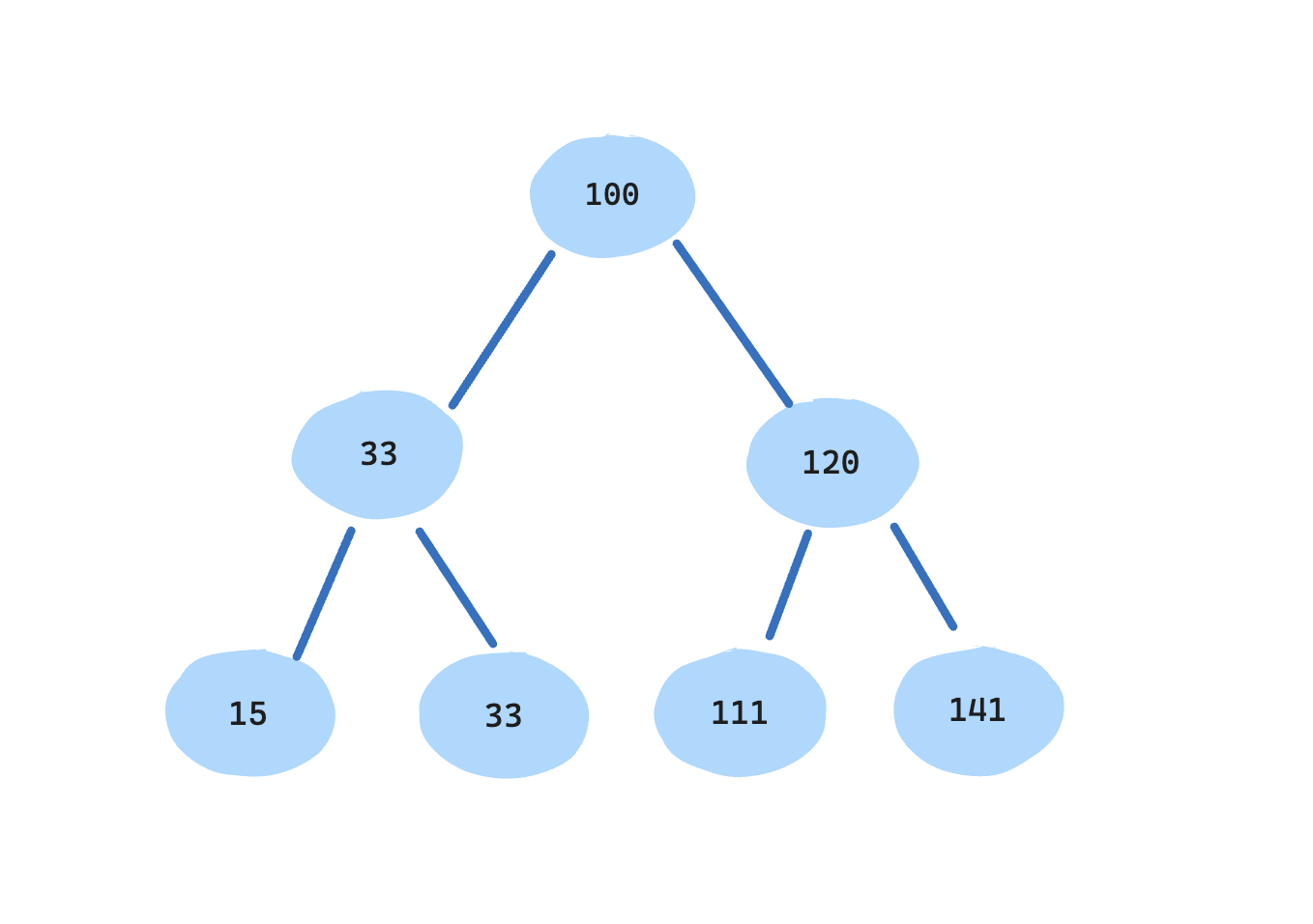
What’s a binary search tree?
This is a note about binary search tree (BST) in JavaScript that I wrote when I was learning it. A binary search tree is a type of binary tree that maintains a specific relationship between nodes. It is named as such because it is particularly effective for searching operations.
A BST must adhere to the following condition for any node:
- The value of all nodes in the left subtree is less than the value of the node.
- The value of all nodes in the right subtree is greater than the value of the node.
This condition allows for efficient searching operations, as the search can be narrowed down to either the left or right subtree based on the comparison of the target value with the current node’s value.
In a binary tree, you can perform the following operations:
- lookup
- insert
- delete
Node
A node is a point in a tree, and in code, we represent a node using a specific structure. For example, in JavaScript, we can represent a node as follows:
class Node {
constructor(value) {
this.left = null;
this.right = null;
this.value = value;
}
} In the example above, left represents the left child node, right represents the right child node, and value represents the value of the node itself.
Now, let’s create a BST. We’ll add a class with three methods: lookup, insert, and delete.
class BinarySearchTree {
constructor(){
this.root = null;
}
insert(value){}
lookup(value){}
remove(value){}
}Insert function
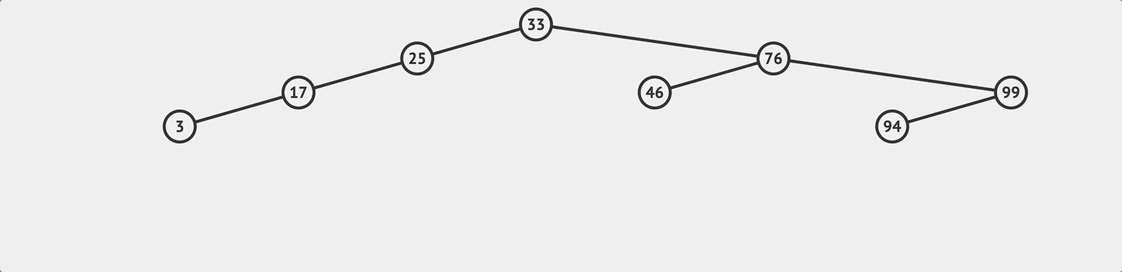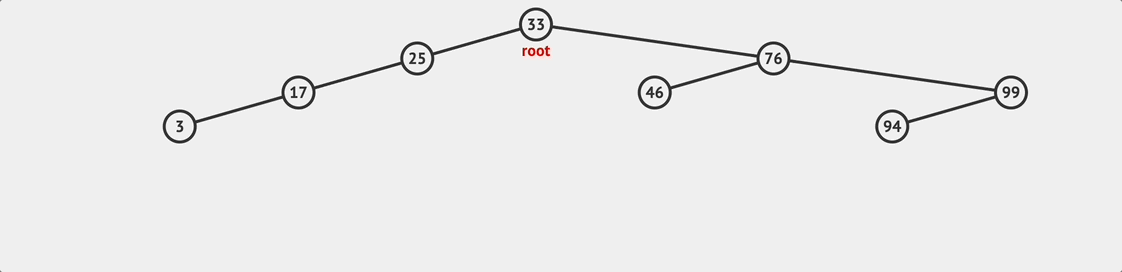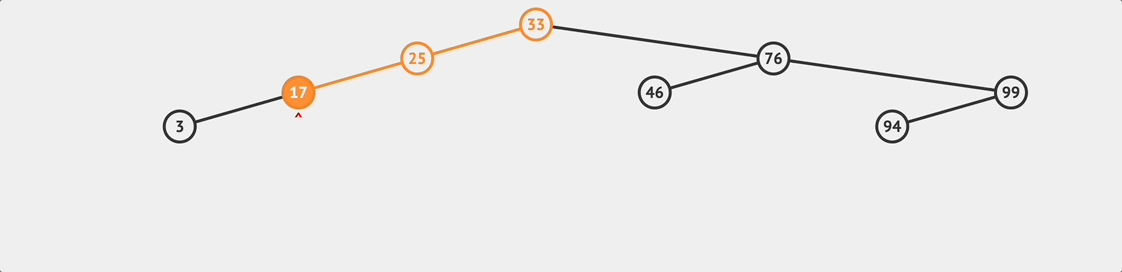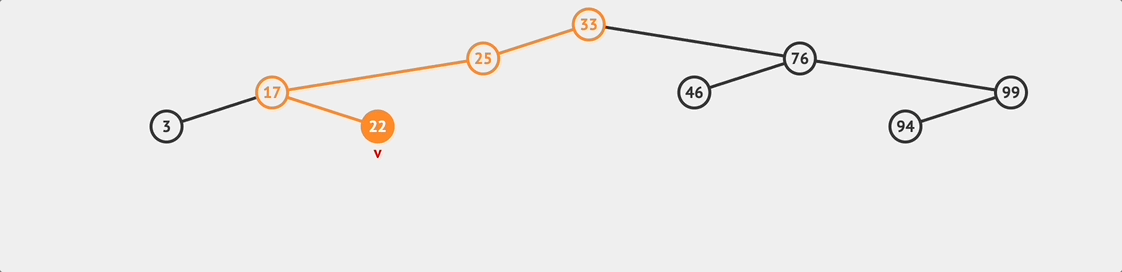 BST insert flow
BST insert flow insert(value){
// create a new node
const newNode = new Node(value);
if (this.root === null) {
this.root = newNode;
} else {
...
}
} Then, we can start searching for the appropriate insertion position based on the value.
Remember the rule of BST?
In a Binary Search Tree (BST), the value of all nodes in the left subtree is less than the value of the node, and the value of all nodes in the right subtree is greater than the value of the node.
We’ll start from the root node and traverse down to find the appropriate insertion position. If the value is greater than the current node’s value, we’ll go to the right subtree. Otherwise, we’ll go to the left subtree.
insert(value){
// create a new node
const newNode = new Node(value);
if (this.root === null) {
this.root = newNode;
} else {
// set the target node to the root
let currentNode = this.root;
while(true){
// compare the value of the new node with the current node
// if the value is greater than the current node's value, go to the right subtree
// if the value is less than the current node's value, go to the left subtree
if(value < currentNode.value){
// check if the left value exists
if(!currentNode.left){
// if it doesn't exist, this is the target position
currentNode.left = newNode;
return this;
}
// if the left value exists, continue to search
currentNode = currentNode.left;
} else {
// if the value is greater than the current node's value, go to the right subtree
// the logic is similar to the left subtree
if(!currentNode.right){
currentNode.right = newNode;
return this;
}
currentNode = currentNode.right;
}
}
}
}Lookup function
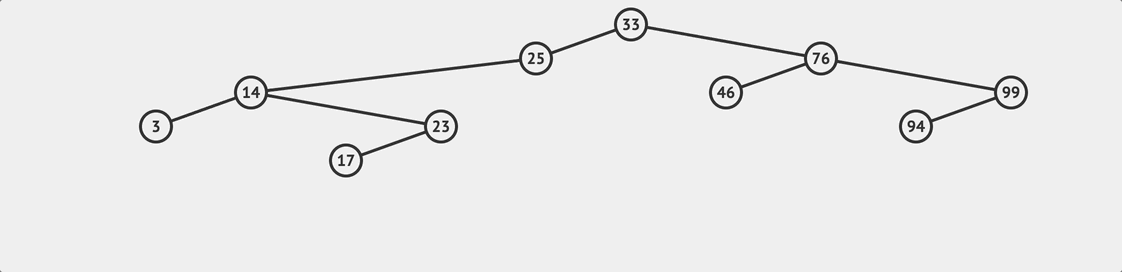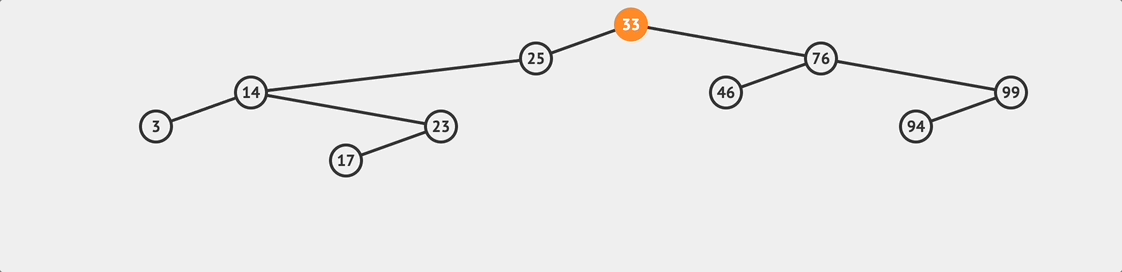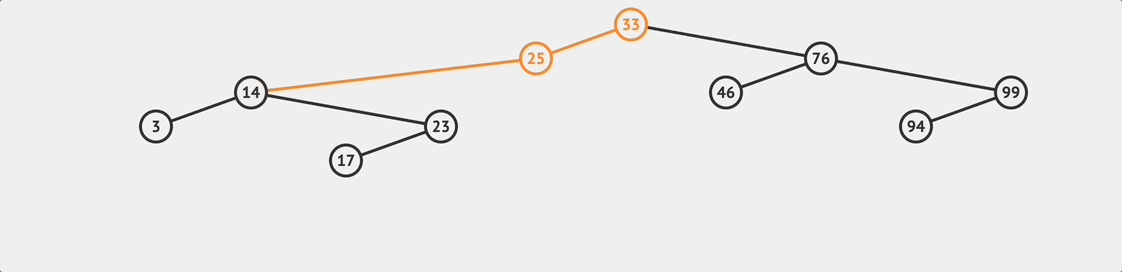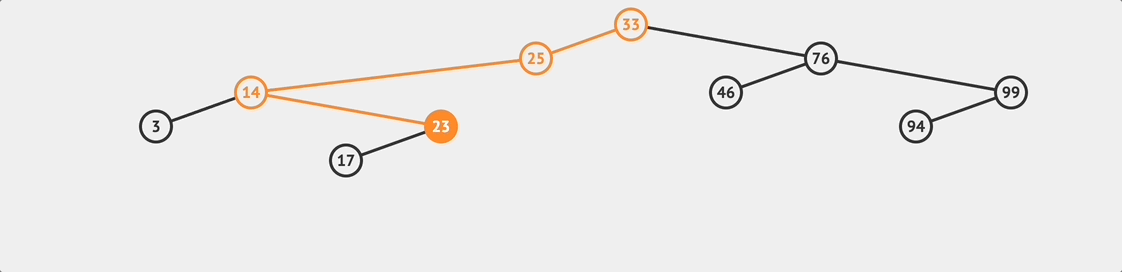 BST loopup flow
BST loopup flow To search for a value in a BST, it is relatively simple. We can follow the BST rules to compare and traverse the tree. The logic is similar to the insert method, starting from the root node and comparing the target value to determine whether to go to the right or left subtree until the target value matches a node’s value.
if we find that currentNode becomes null, it means the target value does not exist in the tree.
...
lookup(value){
if (!this.root) {
return false;
}
let currentNode = this.root;
while(currentNode){
if(value < currentNode.value){
currentNode = currentNode.left;
} else if(value > currentNode.value){
currentNode = currentNode.right;
} else if (currentNode.value === value) {
return currentNode;
}
}
return null
}
...remove
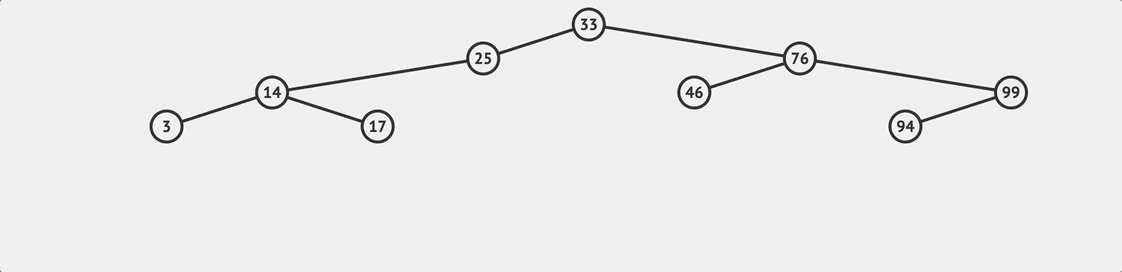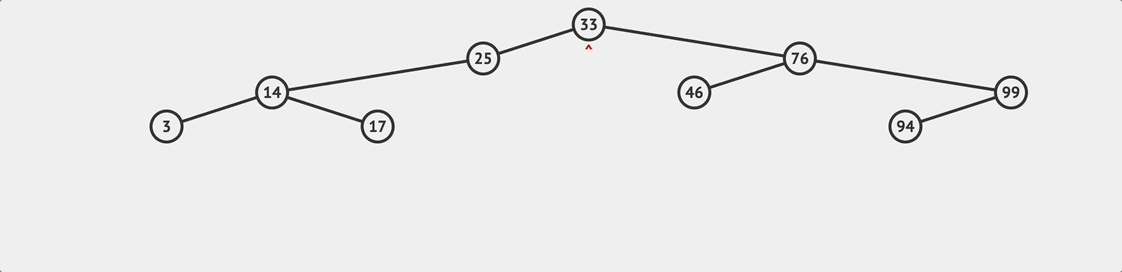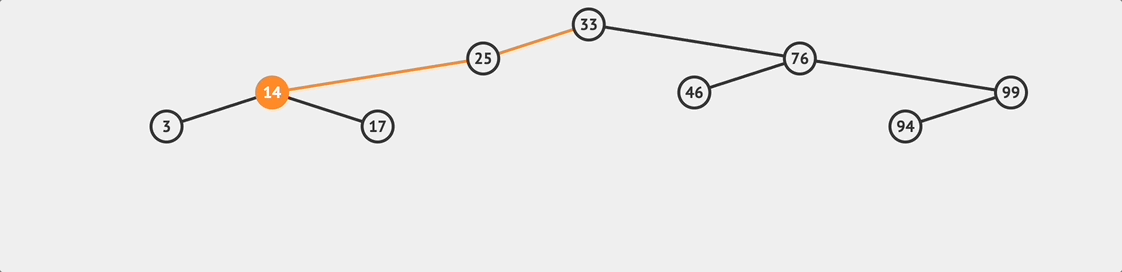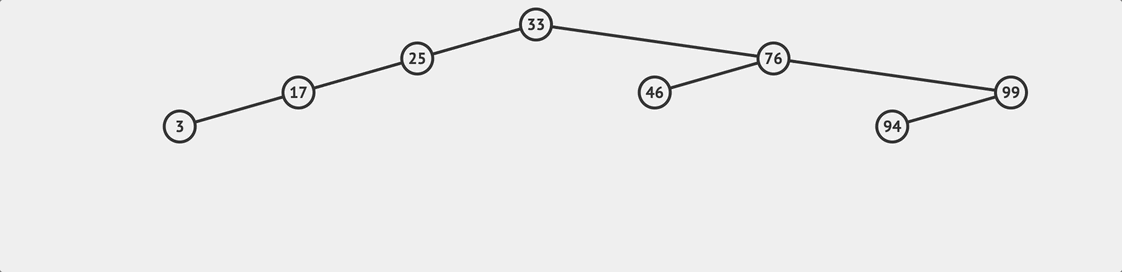 BST remove flow
BST remove flow The last method is to delete a node, which is also a relatively complex method. The delete method can be divided into two steps:
- Find the target node to be deleted
- Remove this node
One thing to be careful about is that if the node we want to delete has other child nodes, we must connect the remaining child nodes and the original tree after the node is removed, as shown in the flowchart above.
So we need to keep track of the parent by using currentNode node while searching.
And we need to keep track of the parent node by using parentNode variable.
remove(value) {
if (!this.root) {
return false;
}
let currentNode = this.root;
let parentNode = null;
while (currentNode) {
// the logic is similar to the lookup function
if (value < currentNode.value) {
parentNode = currentNode;
currentNode = currentNode.left;
} else if (value > currentNode.value) {
parentNode = currentNode;
currentNode = currentNode.right;
} else if (currentNode.value === value) {
...
// find the target node
// the core delete logic
}
}
} And let’s start dealing with the core delete logic!
There might be different ways to implement this, but I’ll use one of them to explain.
First, let’s consider the following three cases (use currentNode to represent the node we are currently looking at):
1. currentNode that doesn’t have right child node
This is the simplest case. If A node only has left child node B,
then after A is deleted, we only need to consider whether B should be assigned to its parent node’s left or right node.
2. currentNode has a right child node that doesn’t have left child node
If currentNode has a right child node that doesn’t have left child node,
then after currentNode is deleted, we will let the right child node take over,
and move the original currentNode’s left child node to the right child node’s left child node.
3. currentNode has a right child node that has a left child node
If our target node to remove has a right child node that has a left child node, we need to find the smallest value in this left subtree (the leftmost node), and let this leftmost node replace the original node. In other words,** we need to find a value that is greater than the original node but smaller than the value of its right child node.**
remove(value) {
...
// } else if (currentNode.value === value) {
...
// find the target node
// the core delete logic
// 1. currentNode doesn't have right child node
if (currentNode.right === null) {
if (parentNode === null) {
// if there is no parentNode, it means the target node is the root node
this.root = currentNode.left;
} else {
// compare the value of the current node with the parentNode
// if the parentNode's value is greater than the current node's value,
// then assign the currentNode.left to the parentNode's left child node
if (currentNode.value < parentNode.value) {
parentNode.left = currentNode.left;
// if the parentNode's value is less than the current node's value,
// then assign the currentNode.left to the parentNode's right child node
} else if (currentNode.value > parentNode.value) {
parentNode.right = currentNode.left;
}
}
// 2. currentNode has a right child node that doesn't have left child node
} else if (currentNode.right.left === null) {
// the left child node of the original currentNode will become the left child node of the right child node after the currentNode is removed
currentNode.right.left = currentNode.left;
if (parentNode === null) {
this.root = currentNode.right;
} else {
// the logic is similar to the previous case
if (currentNode.value < parentNode.value) {
parentNode.left = currentNode.right;
} else if (currentNode.value > parentNode.value) {
parentNode.right = currentNode.right;
}
}
// 3. currentNode has a right child node that has a left child node
} else {
// find the leftmost node in the right subtree
let leftmost = currentNode.right.left;
let leftmostParent = currentNode.right;
while (leftmost.left !== null) {
leftmostParent = leftmost;
leftmost = leftmost.left;
}
// if the leftmost node has a right child node, assign it to the leftmostParent's left child node
leftmostParent.left = leftmost.right;
// assign the left and right child nodes of the currentNode to the leftmost node
leftmost.left = currentNode.left;
leftmost.right = currentNode.right;
if (parentNode === null) {
this.root = leftmost;
} else {
// determine whether the original node's value is greater or less than the parentNode's value
// to decide which child node of the parentNode to assign the leftmost node to
if (currentNode.value < parentNode.value) {
parentNode.left = leftmost;
} else if (currentNode.value > parentNode.value) {
parentNode.right = leftmost;
}
}
}
}
}
}